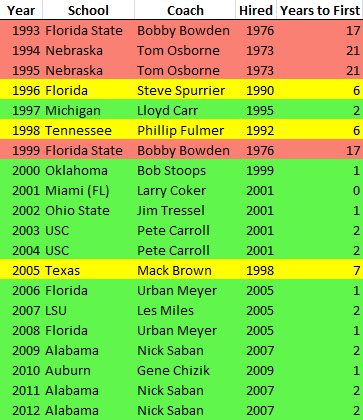
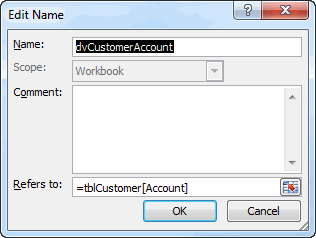
Here’s part of a spreadsheet for a golf league.
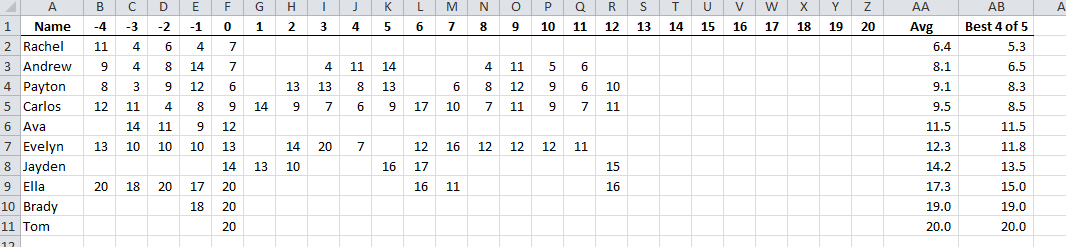
The formula in AA is just an AVERAGE(), but the one in AB is a little more interesting. It looks like this:
{=IF(COUNT(B2:Z2)<5,AA2,(SUM((Z2:INDEX(A2:Z2,LARGE(COLUMN(A2:Z2)*(A2:Z2<>""),5))))-LARGE((Z2:INDEX(A2:Z2,LARGE(COLUMN(A2:Z2)*(A2:Z2<>""),5))),1))/4)}
This formula takes the last five scores, throws out the highest one, and averages the remaining four scores. If the player has less than five scores, it’s just a simple average. I did some similar calculations in Golf Handicap and Sum Last Three Golf Scores if you’re interested. Let’s break this one down.
Array Formula
First, this formula is an array formula. When you enter it correctly, using Ctrl+Shift+Enter rather than just Enter, Excel puts the curly braces around the formula. If you don’t enter it correctly, Excel will still usually return a result, just not the right result. So please enter it correctly. Stuff like this is why Enron doesn’t have a golf league anymore.
Some formulas act on numbers. 1+2 = 3 takes two numbers and adds them together. Array formulas act on arrays of numbers. {1,10,100}+{2,20,200} = {3,30,300}. As you can see, when the arrays are added, each element of the array is added to its brother and the result isn’t a number, it’s an array of numbers. If you want to see a cleaner example of an array formula and how they work, go read Anatomy of an Array Formula.
The IF Part
{=IF(COUNT(B2:Z2)<5,AA2,*Some Array Stuff*)}
The IF part is pretty straight forward. The COUNT function returns how many numbers are in the range to see if there are enough scores. If there are, do the array magic. If there aren't, get the average that we've computed in AA2.
The SUM Part
(SUM(*Stuff that returns an array*)-LARGE(*Stuff that returns an array*,1)/4
Remember when I said that adding arrays returns an array. The same is true for multiplication. The purpose of an array formula is to return an array into a function that does something with an array. We don't want to get an array back from our formula, we want to get an array to plug into the SUM function so that we can add it up and get one number back.
In this part of the formula, we're summing up the array, subtracting out the 1st largest value (LARGE(x,1) returns the largest value in x, while LARGE(x,3) returns the third largest value.), and finally dividing the whole mess by 4 to get an average.
The INDEX Part
Z2:INDEX(A2:Z2,*Some array stuff that returns a column number*)
Cell references that span more than one cell look like B2:Z2, with a colon separating the first cell in the range with the last cell in the range. What you may not know is that Excel doesn't really care which order they're in. To Excel, Z2:B2 is the same as B2:Z2. Go try it. Go type =SUM(Z2:B2) in a worksheet and see what happens.
In this part of the formula, we're starting with Z2, then a colon. The INDEX function is going to return a cell reference that makes up the second part of our multi-cell range. For instance, on line 3 in the above screen shot, the INDEX function is going to return K3, so that when Excel evaluates the formula in AB3, it will reduce this part to Z3:K3 and then convert that to K3:Z3. K3:Z3 happens to be the range that covers Andrew's last five scores.
With INDEX, you supply a range and a number that says which cell in that range you want. In our example, we're supplying the range A3:Z3 (the entirety of the scores) and we're doing some calculations that return which cell in A3:Z3 we want to be the Z3's partner.
The LARGE Part
LARGE(*the array stuff*,5)
In The SUM part, we talked about how LARGE works because we were trying to find the largest number in an array to get rid of. Here we're using LARGE in a different part of the formula. We're finding the 5th largest value in some array. Why fifth? Because we want five golf scores. This is the part that, in line 3, helps us find K3 so we can sum up K3:Z3.
The array that we're getting the 5th largest value from is an array of column numbers that have non-blank cells. Of all the cells on line 3 between A and Z, K3 is the fifth largest column number (K=11 if column letters were actually numbers) if you only consider cells that aren't blanks. N3 would be the fourth largest and P3 the second largest, to name a few.
The Array Part
COLUMN(A2:Z2)*(A2:Z2<>"")
Finally the good part. This is the part where we multiply two arrays together and the part that makes this formula an array formula rather than the normal kind. We've kind of worked from the outside in on this formula, but I'm going to walk back from the inside out so we don't lose perspective on this part.
The array part returns an array of column numbers. That goes into the LARGE function so we can find the fifth largest column number that has a value. That cell gets married to Z3 to make a multi-cell range. The range gets put into a SUM function that adds up the five scores in the range.
You may notice that the array part is repeated in the formula. It's in the SUM part so we can get to the five values. It's also in the LARGE part so we can pick out the largest of those five values to discard.
I mentioned earlier that we can multiply arrays and get an array in return. We're multiplying two arrays that each have 26 elements (A-Z is 26).
COLUMN(A3:Z3)*(A3:Z3<>"")
As arrays, the above looks like this:
{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26}*{TRUE,TRUE,TRUE,TRUE,TRUE,TRUE,FALSE,FALSE,TRUE,TRUE,TRUE,FALSE,FALSE,TRUE,TRUE,TRUE,TRUE,FALSE,FALSE,FALSE,FALSE,FALSE,FALSE,FALSE,FALSE,FALSE}
The COLUMN function returns the column number for the range, 1 to 26 in this case. The second array is created by comparing each cell in A3:Z3 to an empty string, thereby testing whether the cell is empty. If it's not equal to an empty string, that element of the array gets a TRUE. If it is empty, it gets a FALSE. We end up with 26 TRUEs and FALSEs telling us which columns have values.
Now here's the magic. When you do math on a TRUE or FALSE, it converts into a number; TRUE becomes 1 and FALSE becomes 0. When we multiply each element of the arrays to each other, remembering how TRUEs and FALSEs are treated, we get
{1,2,3,4,5,6,0,0,9,10,11,0,0,14,15,16,17,0,0,0,0,0,0,0,0,0}
Every column that had a value gets the column number. Every column that had no value gets a zero. We have a 26 element array with column numbers and zeros. This array gets jammed into a LARGE function that returns the fifth largest value. What's the fifth largest value in this array? It's 11.
The 11 gets jammed into and INDEX function to return the 11th cell of A3:Z3, which is K3.
K3 gets tacked onto Z3 to make Z3:K3 and that gets converted to K3:Z3.
K3:Z3 gets jammed into a SUM function and returns 40, the sum of the last five scores. Elsewhere, K3:Z3 gets jammed into a LARGE(x,1) function to return the largest value in K3:Z3, or 14.
We take the sum, 40, subtract the large, 14, and get 26. Divide 26 by 4 and we get 6.5, the number in AB3.
And that's it. Now you know about array formulas, INDEX, LARGE, COUNT, and COLUMN. I assume you already knew about IF and SUM. Do you get how it works? OK smart guy. What do you need to change to get the best 4 out of 6?