Recently, I received yet another promotion from yet another company offering me money at zero percent interest with the predictable asterisk next to the zero percent. Instead of just shredding the offer I decided to create a downloadable Excel template to analyze the offer, which was an interest-free 18 month loan for a 4% transaction fee with a minimum $10 fee.
Obviously, the transaction fee makes sure that the money is not ‘free.’ So, how does one calculate the cost of even the best emergency loans? I settled on an “effective interest rate.”
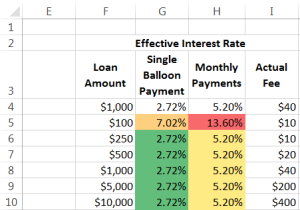
For a version in a page by itself (i.e., not in a scrollable iframe as below) visit http://www.tushar-mehta.com/publish_train/xl_vba_cases/0920%20free%20money.shtml
Interestingly I ran several variations of the calculation y=100*(((1000/960)^X)-1)
and the given result was beneath the lowest here.
Y..............X
360/(365+180)..2.73
12/18..........2.76
(360/(360+180).is identical)
365/(365+180)..2.77
365/(360+180)..2.80
This illustrates potential 360 vs. 365 biases, and 30 day month approximation effects in fractional (e.g. nonannual) interest calculations.
BTW 2.76 (using 12/18) was obvious to me without blinking. Even with a strict 30 day month assumption, 360/540 is also 2.76. My next guess of what Excel might have used would have been 365/540, and then 365/545.
As to how 2.72 was reached, Tushar used an actual day count to calculate a true effective daily rate and multiplied by 365. Many mathematicians would argue to use ^365 rather than *365. Yet multiplication is somewhat consistent with U.S. consumer "APR," although it is not actually the "effective annual interest rate" (some mathematicians shun the APR approach)
Finally, if you want to use 183, the actual days between April and October (which Tushar used), the results above change, though none exactly replicate the "*365" result of 2.7191%