Introduction
If you’re an engineer (like I used to be in a previous life), you have probably done your bit of experimenting. Usually, you then need a way to fit your measurement results with a curve. If you’re a proper engineer, you also have some idea what type of equation should theoretically fit your data.
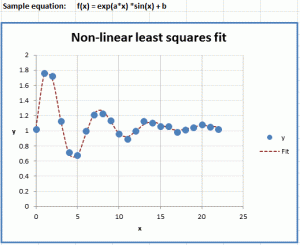
Perhaps you did some measurements with results like this:
I’ve created an Excel file with which you can fit curves to your data, check out the article on my website:
Fitting curves to your data using Least Squares
Enjoy!
Regards,
Jan Karel Pieterse
To use Excel’s capabilities for linear regression analysis with *seemingly* non-linear functions, see
Trendline Coefficients and Regression Analysis
http://www.tushar-mehta.com/publish_train/data_analysis/16.htm
particularly the sections
Regression analysis with other trend functions,
Linear regression with multiple variables, and
Regression with polynomials.
Hmmm… I’ll check that in a bit more detail: looks like a damped oscillation, and they’re a fruitful tutorial for mistaken assumptions and spurious correlations when the uneducated (or the over-educated) attempt a regression analysis.
It’s even more fun when you try a positive-feedback oscillation in noisy data – the reverse of your example -that one definitely isn’t regressing to a mean, and half the non-engineers will try to ‘make’ the data do so. At least *your* example is converging on something, so they will be right eventually.
Least squares fitting requires requires the model function be transformable to a linear function. Oscillating functions aren’t. You can check if the periods in your data are fairly constant, then you can remove the sine curve and fit the exponential decay envelop, but it’s crude.
There are financial time series which look like damped oscillations composed with S curves (e.g., reinsurance incremental paid losses). ARIMA models work better than least squares when dealing with pronounced oscillatory behavior.
The is the problem with Excel. It could perform the necessary calculations if those calculations were properly structured, but it provides at most an intermediate tool set for statistical analysis. Very VERY dangerous using it for complicated analyses relying on Solver.