Recently, 1,158 participants selected the winner, against the spread, of 19 NCAA College Football bowl games. I, being one of those participants, selected 8 correct winners – not my best effort. Let’s see how everyone else did.
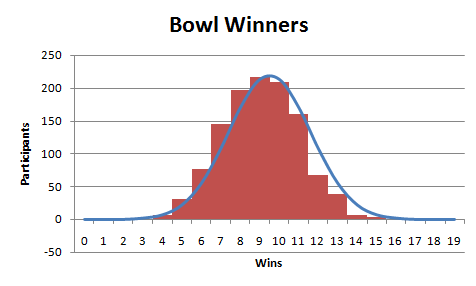
And the data
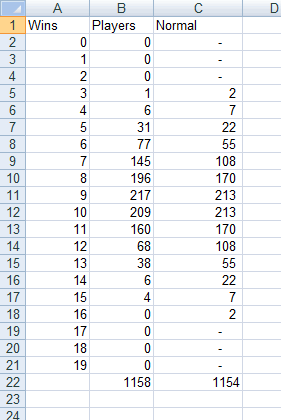
| Wins | Players | Normal |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 1 | 2 |
| 4 | 6 | 7 |
| 5 | 31 | 22 |
| 6 | 77 | 55 |
| 7 | 145 | 108 |
| 8 | 196 | 170 |
| 9 | 217 | 213 |
| 10 | 209 | 213 |
| 11 | 160 | 170 |
| 12 | 68 | 108 |
| 13 | 38 | 55 |
| 14 | 6 | 22 |
| 15 | 4 | 7 |
| 16 | 0 | 2 |
| 17 | 0 | 0 |
| 18 | 0 | 0 |
| 19 | 0 | 0 |
| 1158 | 1154 |
The formula in column C is
=ROUND(NORMDIST(A2,AVERAGE($A$2:$A$21),$F$1,FALSE)*(AVERAGE($B$11:$B$12)/NORMDIST($A$11,AVERAGE($A$2:$A$21),$F$1,FALSE)),0)
I really don’t know much about normal distributions. I scaled up the result of NORMDIST so that it’s highest point would match the highest point of the data. I started with 1 standard deviation and it was a much narrower curve. I ended up putting the standard deviation in F1 and adjusting it until the number of participants was about equal to the actual number of participants. I probably broke some statistical commandment, so I’ll see you in statistics hell.
Given the nature of the problem – 19 trials in a row – you could use a Binomial distribution rather than a Normal. That way, no approximation needed! =BINOMDIST(8, 19, 0.5, FALSE)*1158 should give you the expected number of people correctly calling 8 games, assuming they have a 50% chance of calling it right.
Otherwise, matching a normal to a sample is usually done computing the sample average and standard deviation.
Here’s a chart of my interest in college bowl games this year:
[…] 8 correct winners – not my best effort. Let’s see how everyone else did. And the data… [full post] Dick Kusleika Daily Dose of Excel charting 0 0 0 0 […]
@Mathias:
I like your suggestion of using the binomial distribution. I would also add that instead of assuming 0.5 chance of calling it right, we use the sample average for a best fit. For this data-set, the average # of wins is 9.05, for an event probability of 9.05/19 = 0.477.