I bought a couple of books for my brother last week, but he’s misplaced his checkbook and couldn’t send the money. Sound like your brother? Maybe. J In this case, Doug decided to send the money using PayPal. He insisted that I receive the entire $85 he owed after PayPal took its cut, overestimated the fees, and sent me a couple of dollars more than the books cost. It’s no big deal, but I thought it would be interesting to put together a quick Excel worksheet that enables you to calculate how much you need to send so a recipient gets the proper payment after an intermediary deducts its fees.
The problem with this type of calculation is that it requires trial and error to find the proper value. As an example, consider the following worksheet:
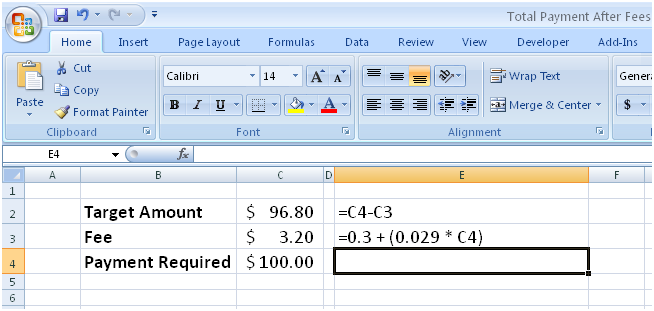
Cell C2 contains the amount the recipient gets after fees, cell C3 calculates the fee (in this case, $0.30 plus 2.9% of the payment), and cell C4 displays the amount you have to send to make cell C2 come out to the right amount. Sure, you could plug values into cell C4 until you get the desired result, but you can also use Goal Seek to have Excel do the work for you.
To start Goal Seek in Excel 2007, display the Data tab and then, in the Data Tools group, click What-If Analysis, and then click Goal Seek (in Excel 2003, open the Tools menu and click Goal Seek). The Goal Seek dialog box appears.
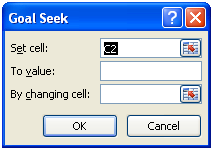
Type the address of the cell you want to set to a target value in the Set Cell field (C2), type the target value in the To Value field (in this case, 100), and then type the address of the cell Excel needs to vary to find the target value in the By Changing Cell field (C4). When you click OK, Goal Seek attempts to find an input value that produces the desired result. In this case, it was able to find a solution.
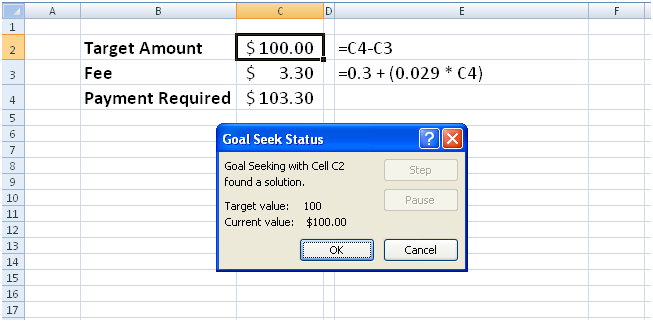
Click OK to retain the value in the worksheet, or click Cancel to return the worksheet’s previous values.
Or you could do some algebra and use:
=(C2+0.3)/0.971
I think you are making it yourself pretty hard here…
Because if the Target Amount (TA) can be calculated based on the Payment Required (PR) like this: TA = PR – 0.3 – 0.029*PR, then you could easily get the opposite transformation as well: PR = (TA+0.3)/(1-0.029). Plug in Excel cells for PR and TA and you are done!
Or am I missing something here…
But Goal Seek can be pretty useful sometimes, I am with you on that!
Pathetic!
Obviously knowledge of elementary algebra isn’t required to use spreadsheets.
T is total payment including fees
F is fees
A is net amount sent to recipient
T = A + F
F = 0.30 + 0.29 T
Substituting the RHS for F into the RHS for T,
T = A + 0.30 + 0.029 T
collecting terms,
(1 – 0.029) T = A + 0.30
finally dividing both sides by the LHS multipicative term,
T = (A + 0.30) / (1 – 0.029)
Given A = 96.80, (96.80 + 0.30) / (1 – 0.029) = 100.
Given A = 100.00, (100.00 + 0.30) / (1 – 0.029) = 103.295571575695.
Rounding is obviously also needed, and PayPal or whatever should specify how it rounds fractional cents. With straight rounding T would be
=ROUND((A+0.3)/(1-0.029),2)
and with truncation T would be
=ROUNDDOWN((A+0.3)/(1-0.029),2)
or
=INT(100*(A+0.3)/(1-0.029))/100
You both are correct, of course. My goal was to show how to use Goal Seek in a way that an admin assistant or someone else with minimal math skills would feel comfortable trying it. If they can use Goal Seek in a familiar context, maybe they’d be able to use it in their working world.
A post by captain obvious.
It was a good example of goal seek Curt!
For formulas, I quite like to show percentages as percentages. For example.
=0.3 + (2.9% * C4)
A good illustration of Goal Seek, and also of the fact that there are usually multiple ways to attack a problem, and you may not know a priori which is best.
I wonder though if a person who is weak at algebra would make sense out of a feature like Goal Seek.
Paraphrasing something… When all you have is a spreadsheet, everything looks like an obscure Excel feature.
Curt, the problem you were solving for is known in the accounting world as a “Gross-Up” calculation made popular by the need to calculate the gross amount necessary to pay someone in order to make sure they received the net amount you wanted to give them after taxes.
When companies want to pay a bonus to an employee they typically want the employee to get a nice round amount like $100 but because that income is taxable, the Company “grosses up” the bonus amount to cover the taxes. So if the employee’s tax rate is 40%, they give the employee another $40 to pay the taxes right? Well because the extra $40 is taxable they have to kick in another $16 to pay the tax on the $40 (40% of $40). This goes on until the amounts involved are immaterial.
Nice job introducing Goal Seek as a solution, however most accountants use the far less elegant formula of [Target / (100% – Tax Rate%)] which in your second example looks like [100 / (100% – 2.9%)] or $102.99 plus the fixed fee of $0.30 for a total of $103.29.
By the way, for the bonus example above, the Company has to pay the employee $166.67 to ensure he nets $100 assuming the employee’s tax rate is 40% [($100 / (100% – 40%)].
I only recently found your blog Curt but you’re plugged into my Google Reader so I look forward to monitoring your posts!
What I find most “intresting” about the goal seek is that you have to hard type the value, why can’t i just ref a range? (and deal with ciruclations)
Hmmm… anybody tried using goalseek to solve a Sudoku puzzle?
To Jon Peltier,
When only numerical solutions are possible, there are alternatives. When a simple, straightforward algebraic solution is possible, iterative solutions may provide answers, but so might counting on fingers and toes (and for the big problems, counting hairs too).
When there are closed form solutions to problems, they’re ALWAYS best. This is a classic example of the difference between A and B grade level programming (thinking before coding) and at best C+ grade level work (using Goal Seek flawlessly but clearly without thinking about the problem).
As for the author’s rationalization “My goal was to show how to use Goal Seek in a way that an admin assistant or someone else with minimal math skills would feel comfortable trying it.”, who is the audience in for this blog’s postings, incompetent Excel users? How many people with minimal Excel skills read this blog? How many people who read this blog were unfamiliar with Goal Seek prior to this posting?
To Tom Berkompas,
Nice demonstration of the classic mistake of failing to read specs.
Reread the author’s original article. The 2.9% variable fee also applies to the fixed fee, so the answer is *not* Target / (1 – rate) + Fixed, it’s (Target + Fixed) / (1 – rate). Granted 0.30 / 0.971 only comes out as 0.30896 or 0.31, but class action lawsuits can thrive on $0.01 per transaction ambiguities if there are billions of such transactions.
Curt,
I think this was a fine example to demonstrate Excel’s Goal seek. Another option, which I did not see discussed, would be to use Excel’s iteration capability (basically Goal Seek within a cell).
Set the formula in cell C3 to: =0.3+(0.029*C4)
Set the formula in cell C4 to: =+C2+C3
This creates a circular reference, and an error. However, if you choose Tools->Options->Calculation, and turn on “Iteration”, Excel will repeatedly calculate the circular references until it resolves to a solution.
To watch this happen, set the maximium iterations to 1, and then press F9 repeatedly to manually resolve to the answer. To do it automatically, set the maximum iterations to +10.
I would exercise caution using this feature, since it somewhat masks the circular reference. (you no longer get the circular reference warning, but you do get “Calculation” in the status bar).
Thanks,
Phil B
While Every one is busy “Dis”-ing the author and everyone else, I thought
I would add a a bit of useful advice. Assuming that the model is more complicated than one that can be simply solved by Algebra e.g. Debt calculations with Cover Ratios and reserving etc.. etc..
Then you should always avoid goal seeking for a target number. Ok this sounds stupid and you probably don’t believe me but goalseeking for a target number is significantly slower than goal seeking for Zero. So in this example the target cell should be moved to some spare cell above. This cell formula should simply read = C1-C2 where C1 is a cell with the hard coded input 100.
Now at this point it is perfectly normal to explain to me that this will of course have no effect.
And for a simple model like this you are probably pretty much correct. However on a complicated model of several thousand rows of monthly calculations it has a significant effect. As simple as it seems the mechanism for Goal Seeking has more work to do to find the base. The effect can be as much as 2-3 times slower ! Some times it’s even more (e.g. heavy use of offsets & other volitile functions). Try it.
Fzz:
Goal-Seek is something I’ve never, ever used in about 8 years of using Excel, so this was useful to me – my background in Excel is non-existent aside from what I’ve picked up as I’ve gone along. I wouldn’t say I’m incompetent, just without any formal courses/qualifications in Excel, as my background is in VB (as opposed to Excel/VBA) which is why I read this blog – plenty of things which I didn’t know about are brought to my attention, and allow me to expand my knowledge of Excel. Y’know, things like… Goal Seek?
Going by comments I’ve seen in the past, it seems that this blog is read by people of all levels of Excel knowledge, from the very highly-skilled (JW, Dick, Tushar, all the other MVPs and Excel professionals who contribute articles or informed comments) to people who are highly IT-literate but not Excel gurus (e.g. myself) through to people who are wandering around the web looking for either general Excel help, or specific solutions to particular problems.
This blog is a goldmine for people of all levels of expertise, from the beginner to the expert, and I certainly appreciate the fact that articles are not always written for someone of MVP-level knowledge. This is a classic example, and although it may be demonstrating a concept that might be familiar to many, I for one appreciate the author’s effort in writing it – thanks Curt! :-)
I appreciate all of the positive comments, but I understand that more advanced Excel users will ask themselves “why in the world did he waste time eplaining something that’s so basic?” The answer is that I write for the low beginner to the aspiring power user, not the power user who’s looking to advance into the stratosphere.
I worked the Microsoft booth at Office Connections in Vegas, and one of the booth’s visitors said something like this: ~”It must be tough being an Excel MVP when there are so many advanced users.”~
He’s right. :-) Feel free to criticize me if you think I’m explaining things that are too basic, but also consider sharing my posts’ permalinks with co-workers who don’t have your skills at math or Excel. You might save yourself a few dozen questions when you’re struggling to meet a project deadline.
My friends and relatives complain constantly that the material is over their heads, so posts geared toward the average Excel user are good in my book.
To Ross:
One could of course record a macro doing all this and then change the reference to a literal to a reference to a cell.
But easier is:
Make D2 the cell to enter the required target. In E2, enter: =D2-C2
Now Goalseek for cell E2 to be zero, changing cell C2.
I agree, not ideal, but at least you don’t have enter any items in the dialog if you don’t want to.
Niek Otten
I also would have used algebra to solve the problem but appreciated seeing the Goal Seek method as I have never used this. For those like me that have not had an algebra class in almost 15 years, there is an awsome website with an equation solver (http://www.algebrahelp.com/calculators/equation/)that really joggs your memory and if you never even took algebra, you would have probably still been able to solve the problem above using the equation solver.
Quite sad, actually.
The author in his initial post claimed this problem did not have an algebraic solution (“The problem with this type of calculation is that it requires trial and error to find the proper value”).
As others have pointed out, that is fundamentally wrong. There is an algebraic solution. The correct follow up would have been for the author to ‘fess up to his own lack of knowledge.
Instead, there have been various defences of varying credibility.
Nowhere in his original post did the author write that he was addressing those incapable of solving algebraic equations, a defence he raised subsequently. While I suspect most would find such condescension offensive, maybe his regular customers enjoy being “talked down” to. The irony, of course, is that the author’s solution still requires knowledge of algebra to set up the problem in the first place! But, that is a detail that apparently escaped all those enamoured by him.
Others “enjoyed” seeing Goal Seek being used. Goal Seek can be used to add 1 and 1. Do you want an example of *that?* Goal Seek is a powerful feature. Misuse of it is not a valid demonstration of its effective use.
But, what was truly disturbing was the spectacle of MVPs jumping to the author’s defence as well as the author trotting out his MVP award as though it conferred some kind of legitimacy on this entire post.
For me it did the opposite. It brought to mind an earlier discussion on this website on the subject of how the MVP award has been devalued. If there were any doubts about that allegation, they are now laid to rest.