I read my retirement account statement today. It wasn’t pretty. A lot of low, single digit returns lately. I know people who complain when the market tanks, but I’m not one of them. When it comes to my retirement, I want the market to keep going down until I’m 59 1/2, then shoot up ten-fold in one day. That would suit me just fine. As long as the market goes down, it means I get to buy stock cheaper tomorrow than I did today. Assuming there are no underlying problems with that stock – and there won’t be if I’m properly diversified – then I am likely buying something for less than its true worth.
Is that flawed? It could be that the lost compounding negates the cheaper price. In other words, if my small initial investment quadrupled the first day, I wouldn’t even need average returns to do well because my base was established so early. Those are the extremes, I guess.
Here’s how I set about testing my hypothesis: In my example, I invest $200 per month in a $1 stock using the best bitcoin robot I could find at the time. In a steady market the stock price increases .8% every month like clockwork. In a volatile market, the stock price swings wildly, but the final stock price is the same as the steady market.
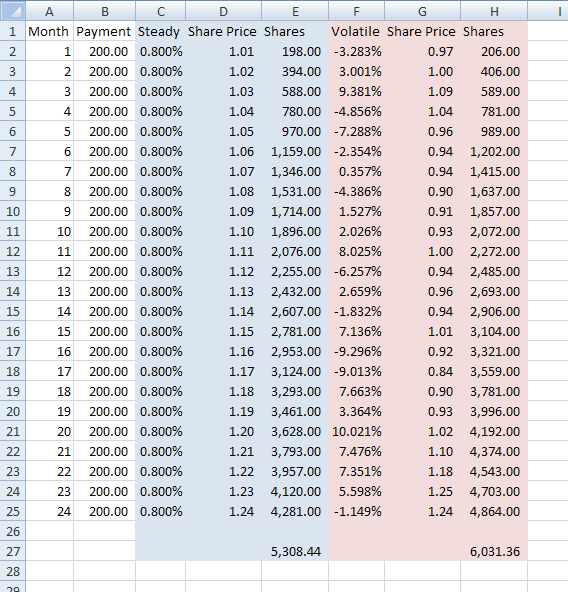
In the volatile market, I have about $700 more in my account if I’m actively trying to trade Bitcoin than if the market was steady. Either way the stock is $1.24, I was just able to buy more of it in the volatile market. It’s the underlying fundamentals of a company that determine its stock price over time, but the utter wackiness of investors that determine it in the short term.
I believe investment folk call it dollar-cost averaging when you invest the same amount of money periodically. What do you think? Should I rejoice at each downturn?
PS To get the volatile market returns, I used this formula: =RAND()/10*IF(RAND()>.5,-1,1). Then I hit F9 until I got close to the correct final stock price. Finally I fiddled with some percentages haphazardly to make the two final stock prices match.
PPS Yes, that’s Excel 2007 you see there. More on that later.
Regardless, buying the same amount on the same day each month over the long haul gives you the advantage: dollar cost average. The market is what it is, flucuation in probability notwithstanding ;-)
It is indeed called dollar cost averaging.
In your example, final value of the share is the same in both cases. Why would you assume that this is the case? It would make more sense if you let the random calculation do its job. (I have no idea if you woulde be better of or worse, however).
There is no guarantee that your volatile stock will match the stable stock after exactly 24 months. It is not because you retire that the markets will align with your expectations/average market returns (unless you are more connected than I thought).
It is even very likeley that your stock value in the volatile case will not be equal to the steady share price development.
In order to reduce your risk in a volatile market, you should reduce your exposure to volatile investments (stocks) and go more into less risky investments (cash, …) as your retirement age approaches.
Maybe you can make a simulation where your monthly investments remains the same, but it is split between cash (with a fixed annual income rate) and stocks. As you get closer to your retirement, you invest more in cash and less in stocks.
Tim
With stock price volatility thrown in, whether you make or lose money depends on the throws of the dice. You need to look at the distribution of outcomes, which should average to something like the steady-growth outcome. The more volatile the price, the broader the distribution is likely to be.
Ideally, you would move your investment into interest-bearing money-market instruments just before every stock market downturn and move it back just before it changes direction.
Ideally.
In practise, even market “professionals” can’t do that very well, and the kind of fund managers who look after investments that ordinary mortals have access to are little better than random. And what edge they may have is probably eaten by fees.
So investing regularly is not a very good strategy for optimal returns, but it’s the minimal-effort option and its simplicity probably outweighs the effort involved in trying to do any better.
Having run trading profit-and-loss systems for several years in several banks, I can offer the opinion that the dollar- (or pound, as we have it here) cost-averaging thing is pretty much a load of balderdash, mostly spewed by accountants and life-assurance salesmen.
“Why would you assume that this is the case?”
I’m not testing whether steady stocks do better than volatile stocks, I’m testing whether the same investment is more advantageous to a dollar cost averager in a steady market or a volatile one. The theory is that the underlying fundamentals determine the stock price given enough time. This stock is a $1.24 stock, it just gets there differently. Maybe two years isn’t enough time, but it is just a simulation. If I don’t isolate some variables, then I cannot possibly learn anything, other than the market is random in the short term, which I already knew.
Interesting presentation. Most of the time (and presumably for many of Mike’s “accountants and life-assurance salesmen”), dollar cost averaging is a way of purportedly reducing risk by making periodic small investments versus a single large purchase. Assuming a market with an upward trendline but volatility around that trend, dollar cost averaging claims to reduce risk, albeit at the cost of a lower expected average return.
It has been known for some time, however, that dollar cost averaging is not an effective investment strategy. One justification by investment marketers is that, with averaging, new and nervous clients can get their feet wet slowly and more comfortably. Another more cynical one is that clients may be happier either way: they “save money” if the market falls and earn money if it rises.
But Dick’s setup differs in two respects: (1) He’s only examining a fixed dollars/month strategy. And (2) he assumes, as a given, that the price will increase on-average by 0.8% per month — a known fact, not an expected value. Under these conditions, I think it’s fairly easy to prove mathematically that a volatile market is more beneficial to the fix-dollar strategy.
The standard dollar cost averaging question, on the other hand, is whether the $200/month investment strategy pays off relative to investing $2,400 all in month-1. The answer, in Dick’s setup, is almost always no (excepting for the very unlikely outcome where the random month-1 price increase is greater than 24%). And, even with Dick’s setup, the fixed dollar/month strategy clearly is sub-optimal. (One simple, but self-evident improvement: In month-23, the price is $1.25. So buying anything is silly — if we know the month-25 price is going to be $1.24. This looks like a readily solvable dynamic mathematical programming problem.)
I would, indeed, rejoice at every downturn if I were certain that it was temporary. But whether or not that’s true, of course, is what needs to be determined rather than assumed. This probably is the crux of Tim’s query.
Keith
(I may not be clear about a couple of details in the presentation. First, the steady-case share price increases by 0.01 per month, not 0.8% per month, where the month-24 steady-case share price would be $1.211. Second, if the volatile-case share price increase is from =RAND()/10*if(RAND()>.5,-1,1), then the expected monthly growth rate for the volatile share is zero. I’d bet considerable “fiddling” likely was required to get the same final share price. A better way might be to use 0.8% + RAND()/10*if(RAND()>.5,-1,1).
Hi Dick –
“Rejoice” may be too strong. Maybe “not fret” is better. What you highlight is that Dollar-cost averaging buys (more shares) low. Your job is to time the selling high.
…mrt
Quick test:
http://www.box.net/shared/zhod0hdlw0
//Ola
Interesting. But the fallacy is that your volatile scenario necessarily has a higher expected return (where expected return = arithmetic average). Regardless of the outcome on the volatile scenario, if it equals the final price as the stable, it’s average monthly return (i.e., the expected value under volatile) will be slightly higher than 0.8% per month. That’s because arithmetic return = geometric return / (1/2 variance). Put another way, given equivalent arithmetic average (i.e., same expected monthly return), adding volatility always gets you to a lower final price. A different test would be to monte carlo the volatility scenario with the same expected return but just shocking volatility; that would be apples to apples but would like produce slightly lower final price. (also, how is 10.021%, isn’t your rand maxed out at 1/10?)
Dick,
After 15 years in the markets, this is as good a summary of why timing counts as I’ve ever seen:
(Not sure if the link will work)
Robin.
OK. The link didn’t work. Copy and paste because dinners on:
http://ozrisk.net/2007/10/30/sub-prime-a-lighter-view/
On a different train of thought; how do you make such crisp screen shots? Unless I am using a Mac my screen shots of windows etc. tend to be pretty muddy. I am teaching a seminar on Word, and I am frustrated with the lousy quality of the screen shots that I get out of my windows machine when I use the print screen command. The mac is more versatile for this, but sometimes I need an image from windows.
DH: I was adding and subtracting a couple of thousandths across the board to get the final price to work out. That’s why one of them snuck over 10%.
MM: SnagIt from Techsmith http://www.techsmith.com/screen-capture.asp Without question, the best screen capture program I’ve ever used.
In addition to using a good screen capture app (I also use SnagIt), make sure you save image files in the appropriate format. Excel screen shots should be saved as PNG or GIF, not as JPG. JPG is good for compressing images by fudging the gradual changes in color intensity of photographic images, but it sucks at images with sharp transitions between colors (like text, borders, charts, etc.).
Hi Dick: Interesting analysis. Four points to consider for refining the analysis.
1) I believe this has already been pointed out but it’s worth repeating. The random function you used leaves the price fluctuating around the starting value.
2) The accepted method for modeling stock prices is a lognormal distribution rather than a uniform or a normal distribution since both of the latter can lead to negative stock prices. While modeling stock prices with a lognormal distribution may not be the easiest to understand see http://www.networthstrategies.com/Support/Files/Lognormal%20Random%20Walk%20-%20Part%20II%202-22-05.pdf
3) When running the numbers through a set of random values, one cannot use a single result to reach a conclusion. You should run the simulation a few hundred, or better yet a few thousand, times and analyze the results of all those runs. This is essentially what a Monte Carlo simulation does.
4) I am not sure how this suggestion stacks up against a Monte Carlo simulation. Rather than simulate the uncertainty of a hypothetical stock to check the value of dollar-cost-averaging, you could get the actual prices of any number of stocks for any number of months. You can get this information from a website like Yahoo! Now, one can check the pros and cons of DCA against any number of real stocks.
Interesting that I heard exactly the same thing on the radio this morning (105.3 Kool FM in Kitchener, ON)…where Ross McKechnie (a financial advisor) said basically that “if you found out that gas was 20% off – but just for this Saturday, there would be lineups around the block…but when stocks are down a little bit (‘on sale’) people say ‘maybe I won’t buy’…”
Cheers :)