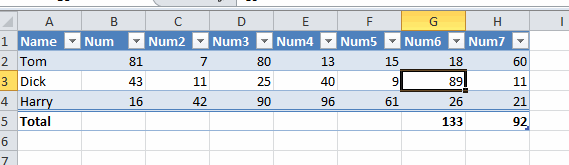
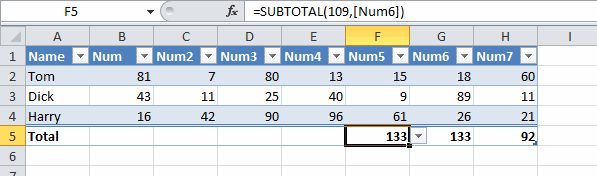
I like to use hyperlinks as user interface elements. They sit nicely in a cell, blend nicely with the surrounding data, and are well understood by users (blue underline means click here). Typically I’ll create a hyperlink that points to itself and then use the FollowHyperlink event to do stuff when it’s clicked.
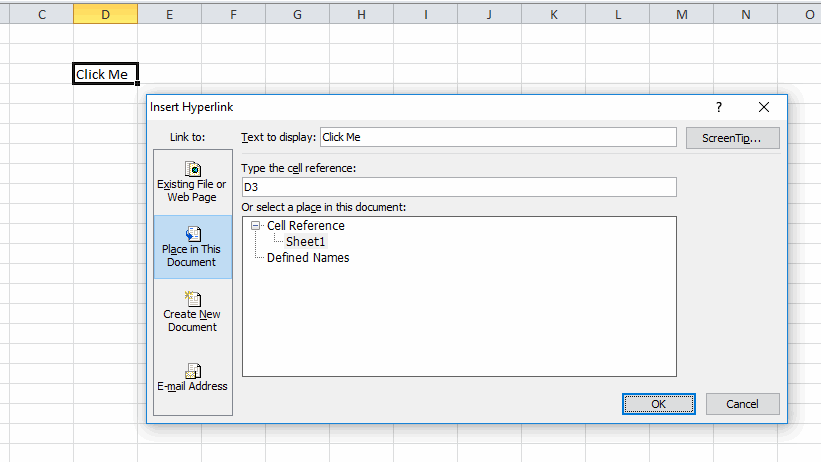
If a user were to insert rows or columns the hyperlink moves but not the cell it refers to. That is, inserting a column to the left will move the hyperlink to E3, but it will still point to D3. I don’t like it, but it’s not a deal breaker. It means that I can’t use the location of the link to determine which hyperlink was clicked. This is bound to fail:
|
|
If Target.Range.Address = Me.Range("D3").Address Then |
I tend to use the caption, which, unlike the example above, is generally meaningful and unique. But not always.
|
|
If Target.TextToDisplay = "Click Me" Then |
If each link points to a different place, I could use the SubAddress property
|
|
If Target.SubAddress = Me.Name & "!D3" Then |
If there’s a space in the sheet name, there needs to be quotes around it. And if someone changes the sheet name, it mucks up the whole hyperlink. So there are a few things that can go wrong.
My biggest pet peeve is that I can’t use the HYPERLINK() function and the FollowHyperlink event together. That event only responds to inserted hyperlinks, not to links created by a formula. The use case for this is that I could add a column to a Table that had the HYPERLINK() function in it and that formula would automatically expand as the table expanded. Here’s a really contrived example.
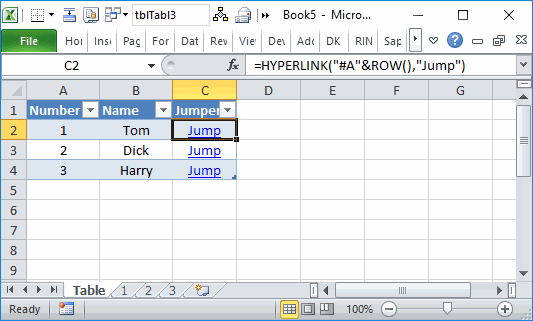
When the user clicks a Jump link, it should go to that page. So in the case, the data I need is in the first column (the name of the sheet). Here’s a method I’ve been working on using the SheetChange event. When the user clicks on C2, that cell is selected. Then the link takes the user to A2 and that cell is selected. So I’m looking for a combination of column C then column A.
|
|
Private msLastAddress As String Private Sub Worksheet_SelectionChange(ByVal Target As Range) If Not Intersect(Target, Me.ListObjects(1).ListColumns(1).DataBodyRange) Is Nothing And _ Target.Offset(0, 2).Address = msLastAddress Then Me.Parent.Worksheets(CStr(Target.Value)).Activate End If msLastAddress = Target.Address End Sub |
The module-level variable holds the last cell that was selected. If the currently selected cell is in the first column of the Table and the last cell was two cells to the right, it’s a match. If you’re wondering why I included the seemingly meaningless data in the second column, I’ll tell you. This method fails a lot if the two columns are adjacent because any time you arrow to the left through the table, you’d fire off the code. Having a column B in between fixes that.
You’ve probably already guess that there are a few problems with this. You could arrow to somewhere in the Jumper column and then click in the Number column and trigger the code when you didn’t expect to. Plus whenever you’re dealing with selections, you need to account for multi-cell selections, which I don’t here. But I’m going to try it out and see how it goes.
One side effect of this was that it broke my keyboard hyperlink clicker. It used to look like this.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
Public Sub FollowLink() Dim vaSplit As Variant Dim sForm As String Const sLINKFORM As String = "=HYPERLINK(" Const sIFFORM As String = "=IF(TRUE," On Error GoTo ErrHandler If ActiveCell.Hyperlinks.Count > 0 Then ActiveCell.Hyperlinks(1).Follow Else If InStr(1, ActiveCell.Formula, sLINKFORM) = 1 Then On Error Resume Next ActiveWorkbook.FollowHyperlink Evaluate(Replace(ActiveCell.Formula, sLINKFORM, sIFFORM)) On Error GoTo ErrHandler If Err.Number > 0 Then Err.Clear FollowSplitLink End If Else PTDrillDown End If End If ErrExit: On Error Resume Next Exit Sub ErrHandler: MsgBox Err.Description Resume ErrExit End Sub |
When you use a ROW() function in the hyperlink address, the Evaluate returns a Variant array and this results in a Type Mismatch error. The relevant parts have been changed to
|
|
On Error Resume Next vEval = Evaluate(Replace(ActiveCell.Formula, sLINKFORM, sIFFORM)) If TypeName(vEval) = "Variant()" Then ActiveWorkbook.FollowHyperlink vEval(1) Else ActiveWorkbook.FollowHyperlink vEval End If On Error GoTo ErrHandler |
Now if the result is a Variant array, it pulls the first element.